算法小结

数据结构

链表

虚拟节点

链表设置虚拟头结点dummyhead，这样对链表来说，第一个元素就是dummyhead的next所对应的节点元素，而不是dummyhead所对应的节点元素。

dummyhead位置所对应的元素是根本不存在的，这只是未来我们编写逻辑方便而出现的一个虚拟头结点。

dummyhead就是索引为0的这个位置的元素的前一个节点。当我们有了dummyhead后，为链表添加一个元素，就不需要对头结点进行特殊处理了，只需要找到等待添加位置的前一个位置的节点，

此时对于链表来说，所有位置都有前一个节点。

反转法

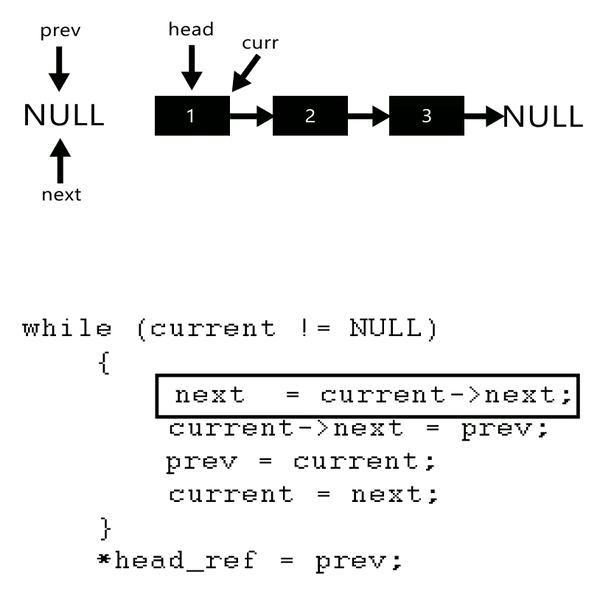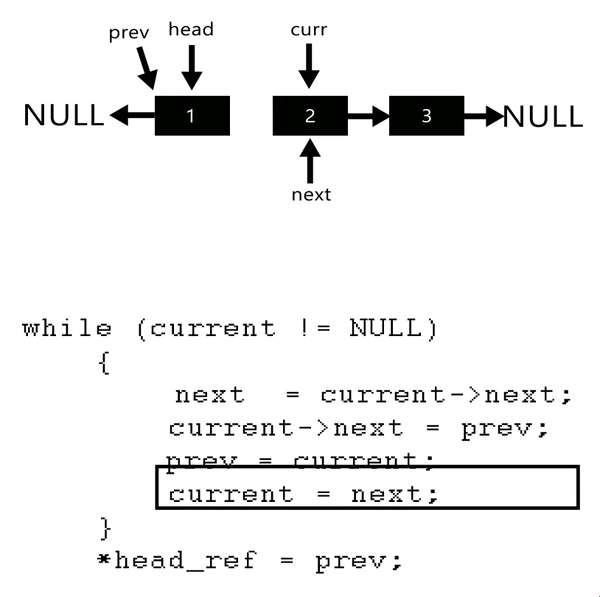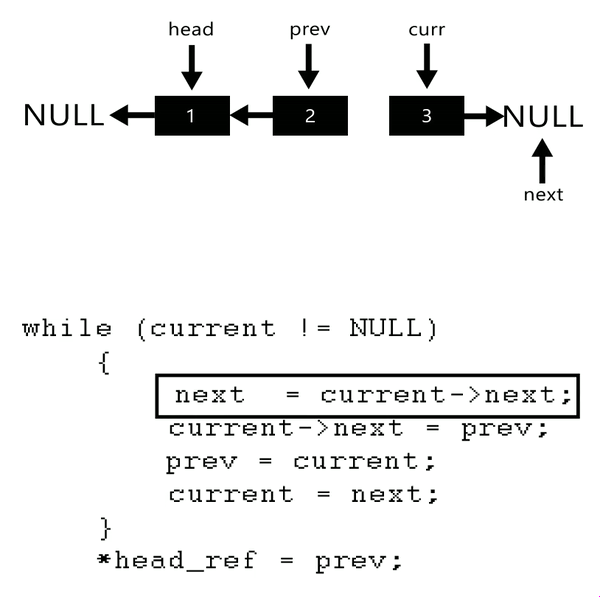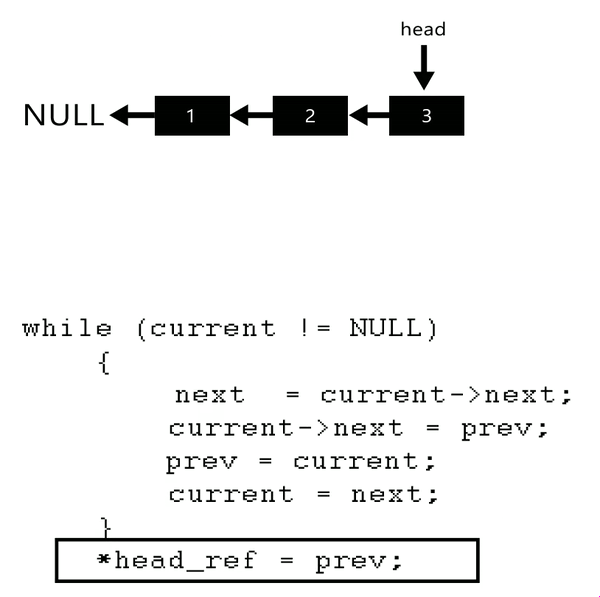
反转的方法很简单:切出一个要反转的头节点,next置为null,作为尾节点的开始.然后不停的将头结点放入尾节点之前.

头插法

这种方法类似于麻将洗牌,可以将自己的手牌当做链表,反转动作可以认为,我们要将手牌中的一张牌插入前面的牌的位置当中.
1.拿出这张牌
2.此时缺了空位,待插入位置整体向后移动链接空位之后的牌,腾出待插入的位置.
3.插入的牌链接空位之后的牌
4.头牌链接插入的牌
图片以反转链表II的拿过来,真正的翻转链表需要g是指向dummynode.

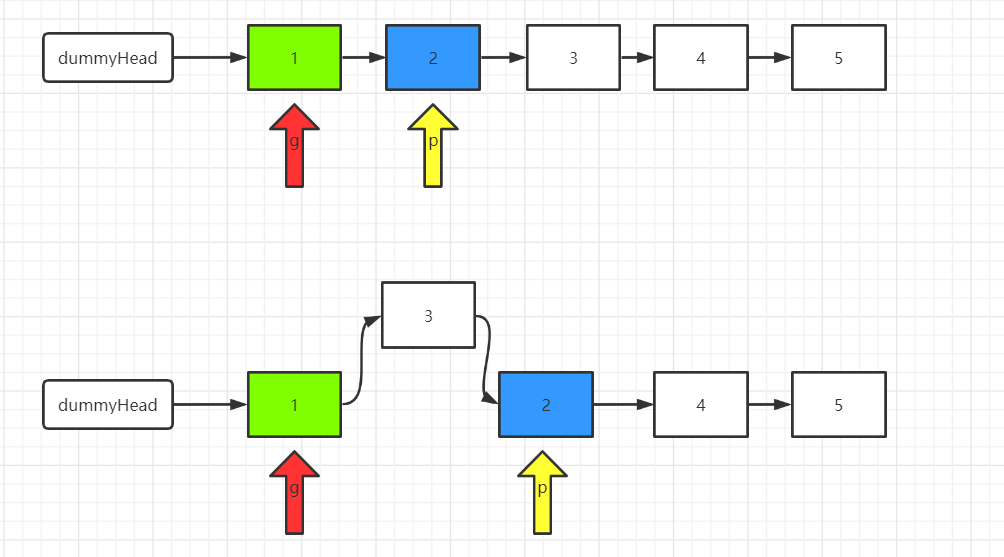
首先要构建一个dumynode,然后以插牌的方式进行构建.g不会动只有p在动,这与上述的反转法,是有区别的.

while(p.next != nil) {
            ListNode removed = p.next;
            p.next = p.next.next;

            removed.next = g.next;
            g.next = removed;
        }

树

广度遍历

1.非递归用,双向链表或者队列实现.

printLevelorder(tree)
1) Create an empty queue q
2) temp_node = root /*start from root*/
3) Loop while temp_node is not NULL
    a) print temp_node->data.
    b) Enqueue temp_node’s children (first left then right children) to q
    c) Dequeue a node from q and assign it’s value to temp_node

2.递归很简单,按层级遍历,但是要注意以下发放效率很差,远不如非递归的实现,方法需要改进.

/*Function to print level order traversal of tree*/
printLevelorder(tree)
for d = 1 to height(tree)
   printGivenLevel(tree, d);

/*Function to print all nodes at a given level*/
printGivenLevel(tree, level)
if tree is NULL then return;
if level is 1, then
    print(tree->data);
else if level greater than 1, then
    printGivenLevel(tree->left, level-1);
    printGivenLevel(tree->right, level-1);

深度遍历

递归版本很简单,非递归的版本.
1.后续遍历,双栈实现.
1.前序遍历,单栈实现.

栈

入栈的元素可以是数组的下标或者是元素.或者可以设计一种KV的数据结构保存入栈的元素.

涉及到距离的题目一般需要存储下标位置.

单调栈-递减栈

站内元素是顺序的,栈顶到栈底整体由小到大.

单调栈-递增栈

站内元素是顺序的,栈顶到栈底整体由大到小.

Hash

hash结构是一种比较特殊的数据结构,key-value映射的数据结构.一般碰撞发生后语言底层会进行处理.

前缀和

区间的问题几个思路供参考：1、滑动窗口（双指针） 2、前缀和的差 3、线段树（树状数组）

前缀和的差值计算,就涉及到前缀计算结果的存储那么就需要用到hash表结构进行存储.

操作

双指针

涉及到数组有序的首先要想到的是双指针能不能实现
一般的双指针根据运动方向分成两种:
1.指针一起从左到右移动(前缀和,滑动窗口上面也有介绍)
2.指针从两边向中间移动(二分,交换元素等)

根据移动的速度
可以分为快慢指针,一般快指针运动速度是慢指针的两倍.快慢指针一般在连表当中很常见.

二分

二分是一种重要的思路,无论是在有序或者无序的输入中查找都能用到.
最重要的判断使用二分的方法是:能否将输入元素分成两部分,其中结果只应出现在其中的一部分,递归下去就可以得到结果.

二分法要注意起始的边界,关建点是起始边的界定义,也就是你要二分查找的范围.

二分在二维有序数据的处理本质上是分两拨,在二维数据集里进行分拨查找.

这些概念有点抽象只能自己慢慢体会.

二分模板

int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1; //长度的边界条件

    while(left <= right) { //注意边界条件
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // left指针向右移动
        else if (nums[mid] > target)
            right = mid - 1; // right指针向左移动
    }
    return -1;
}

为什么while里写的是 <=, int类型的除法需要注意的是只会向下取整,比如[left => 0,right => 1].这样会导致问题的发生.mid=0检查完后,left=1 如果while语句写的是小于,那么会引起问题的产生, right节点就不会检查到了. <= 是确保left与right指针能够相遇,

最主要还是要理解搜索区间的概念,如果按照while <的条件那么有些情况是需要注意的,根据指针移动的规律上下条件有三种::
注意 left= 0, right = len(nums)
mid = ( right + left ) /2

1. 确定下边界

while left<right: 
    mid >= target: 
        right = mid;
    mid < target: 
        left = mid + 1 
nums[left] == tartget? left :-1

2. 确定上边界

while left<right:
    mid <= target: 
        left = mid + 1; 
    mid > target: 
        right = mid;
nums[right - 1] == tartget? right - 1: -1

数学

模

同余定理

给定一个正整数m，如果两个整数a和b满足a-b能够被m整除，即(a-b)/m得到一个整数，那么就称整数a与b对模m同余，记作a≡b(mod m)。

也就是说(a-b)%m == 0 那么就等价于 a%m == b%m.

这在我们处理涉及到余数相关的问题有着巨大的帮助.

动态规划

试用条件

• 最优化原理:
  最优化原理可这样阐述：一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质

• 无后效性
  将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历史的一个完整总结。这就是无后向性，又称为无后效性。

• 子问题重叠
  动态规划算法的关键在于解决冗余，这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术，它在实现的过程中，不得不存储产生过程中的各种状态，所以它的空间复杂度要大于其他的算法。选择动态规划算法是因为动态规划算法在空间上可以承受，而搜索算法在时间上却无法承受，所以我们舍空间而取时间。

解题方法

暴力的递归解法 -> 带备忘录的递归解法 -> 迭代的动态规划解法。

找到状态和选择 -> 明确 dp 数组/函数的定义 -> 寻找状态之间的关系。

组合问题划分

组合问题公式

dp[i] += dp[i-num]

True、False问题公式

dp[i] = dp[i] or dp[i-num]

最大最小问题公式

dp[i] = min(dp[i], dp[i-num]+1)或者dp[i] = max(dp[i], dp[i-num]+1)。

背包问题

背包问题的关注点在于,背包容积的关系,由前一个背包容积推导到下一个背包的容积的问题.
注意背包相关问题的典型就是参数是一个整型用于构建动态规划的二维表.
背包问题具备的特征：给定一个target，target可以是数字也可以是字符串，再给定一个数组nums，nums中装的可能是数字，也可能是字符串，问：能否使用nums中的元素做各种排列组合得到target。

一般思考的思路

• 递归求解：由于有大量重复子问题，因此必须使用缓存，以避免相同问题重复求解，这个方法叫记忆化搜索，在《算法导论》这本书上也把它归入到动态规划的定义中。这种思考问题的方式是从上到下的，直接面对问题求解，遇到什么问题，就解决什么问题，同时记住结果；

• 动态规划告诉了我们另一种思考问题的方式：从底向上，可以不直接面对问题求解，从这个问题最小的样子开始，通过逐步递推，至到得到所求的问题的答案。

0-1 背包问题

如果是0-1背包，即数组中的元素不可重复使用，nums放在外循环，target在内循环，且内循环倒序；
倒序是为了解决覆盖的问题,不能先求j - nums[i],那么这样的话j-nums[i]已经放入了nums[i]，在之后的求解中会重复利用该元素求解结果，导致结果错误。

for  i := 1; i < len(nums); i++
    for j := target; j >= nums[i - 1]; j--

完全背包问题

如果是完全背包，即数组中的元素可重复使用，nums放在外循环，target在内循环。且内循环正序。
正序是因为本次循环要利用上个原素的信息，物品是重复可以使用的。

for  i := 1; i < len(nums) 
    for j := nums[i - 1]; j <= target; j++

顺序问题

如果组合问题需考虑元素之间的顺序，那应该当成排列问题，需将target放在外循环，将nums放在内循环。
原因：

在不考虑物品排列的情况下，我们通常先遍历物品，再遍历背包容量。这是因为对于每个物品，我们都需要在其不放入背包和放入背包两种情况下做选择，而这个选择依赖于背包的剩余容量。所以我们需要先确定物品，再确定背包容量。

在考虑物品排列的情况下，我们通常先遍历背包容量，再遍历物品。这是因为每个物品可以被多次选择，所以我们需要在每种背包容量下，考虑所有的物品。所以我们需要先确定背包容量，再确定物品。

for i := 1; i <= target; i++
    for j := range nums
```    

# 贪心算法

贪心问题和动态规划不同点是:动态规划最终的最优解是由子问题最优解**推导**过来,子问题的最优解不一定是最终问题的最优解,而贪心算法的最优解是子问题的最优解得出的,在一定程度上可以理解为贪心算法的最优解其实就是在计算子问题的最优解.
1、贪心选择性质
一个问题的整体最优解可通过一系列局部的最优解的选择达到，并且每次的选择可以依赖以前作出的选择，但不依赖于后面要作出的选择。这就是贪心选择性质。对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解。
2、最优子结构性质
当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心法求解的关键所在。在实际应用中，至于什么问题具有什么样的贪心选择性质是不确定的，需要具体问题具体分析.


## 特点

1.不依赖动态规划的表结构.
2.不依赖历史决策信息.(历史决策信息不需要保存)



## 动态规划和贪心算法的区别

贪心算法：
1.贪心算法中，作出的每步贪心决策都无法改变，因为贪心策略是由上一步的最优解推导下一步的最优解，而上一部之前的最优解则不作保留。
2.贪心法正确的条件是：每一步的最优解一定包含上一步的最优解。
动态规划算法：
1.全局最优解中一定包含某个局部最优解，但不一定包含前一个局部最优解，因此需要记录之前的所有最优解
2.动态规划的关键是状态转移方程，即如何由以求出的局部最优解来推导全局最优解
3.边界条件：即最简单的，可以直接得出的局部最优解

## 尾递归

尾递归是一种在函数return时的递归调用的方式.这样编译器会优化执行,当前的栈是更新的,而不是新增一个栈执行这段代码.因此涉及到尾递归调用的空间复杂度没有正常递归的空间复杂度高,**因此需要注意** .

非尾部递归,当前栈不能更新,需要保存当前执行状态.
``` js
function recsum(x) {
    if (x === 1) {
        return x;
    } else {
        return x + recsum(x - 1);
    }
}

recsum(5)
5 + recsum(4)
5 + (4 + recsum(3))
5 + (4 + (3 + recsum(2)))
5 + (4 + (3 + (2 + recsum(1))))
5 + (4 + (3 + (2 + 1)))
15

尾递归:

function tailrecsum(x, running_total = 0) {
    if (x === 0) {
        return running_total;
    } else {
        return tailrecsum(x - 1, running_total + x);
    }
}

tailrecsum(5, 0)
tailrecsum(4, 5)
tailrecsum(3, 9)
tailrecsum(2, 12)
tailrecsum(1, 14)
tailrecsum(0, 15)
15