读《深度学习的数学》 笔记-涌井良美
本文有大量的公式图片截图,造成字体大小不统一,给读者带来的不便请谅解.
第一章神经网络和深度学习
神经网络
神经网络来源生物学上的神经元。
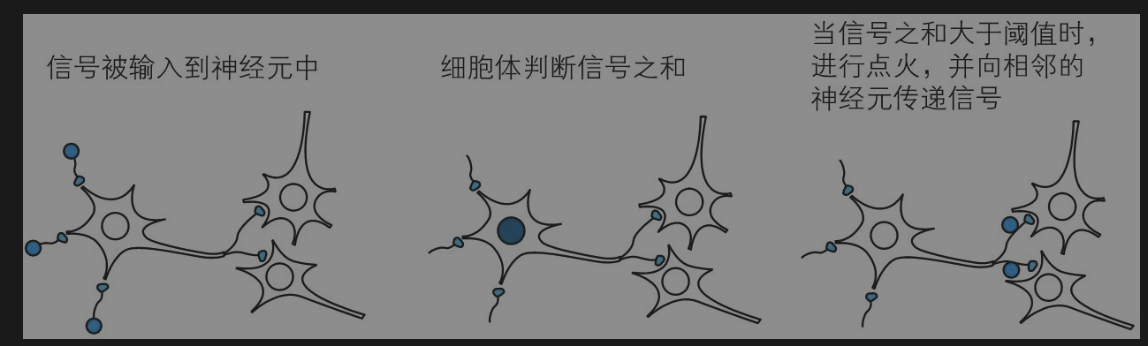
神经元数学表示
神经元根据不同的输入增加权重判断,然后决定输出信号。
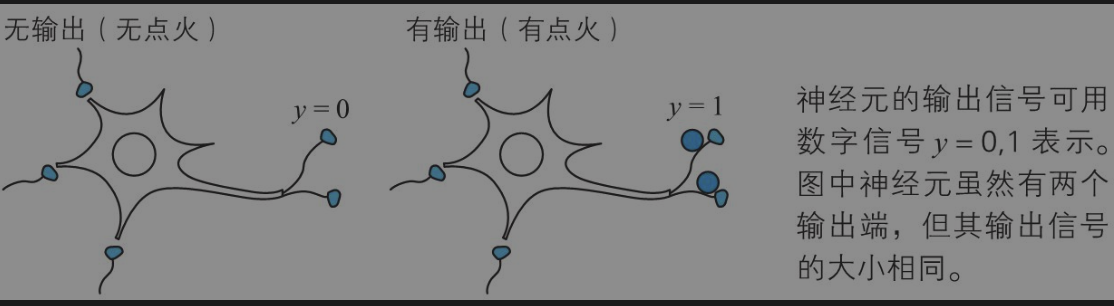
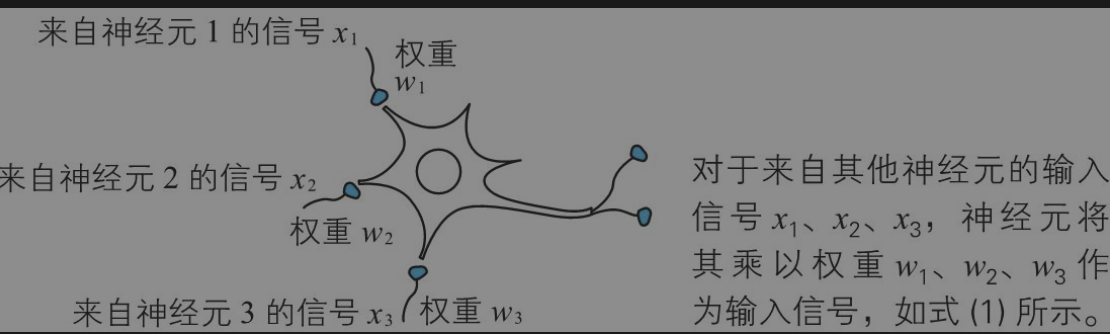
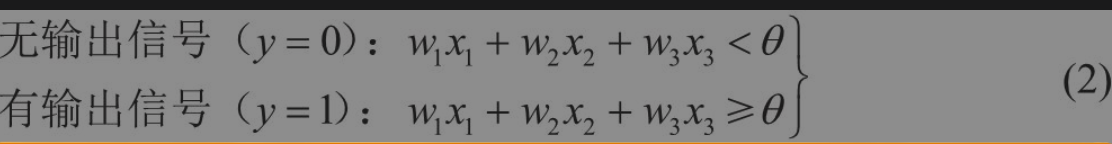
激活函数
激活函数是为了控制每个神经单元的输出函数,将神经网络中的神经单元和生物学中的神经单元关联。
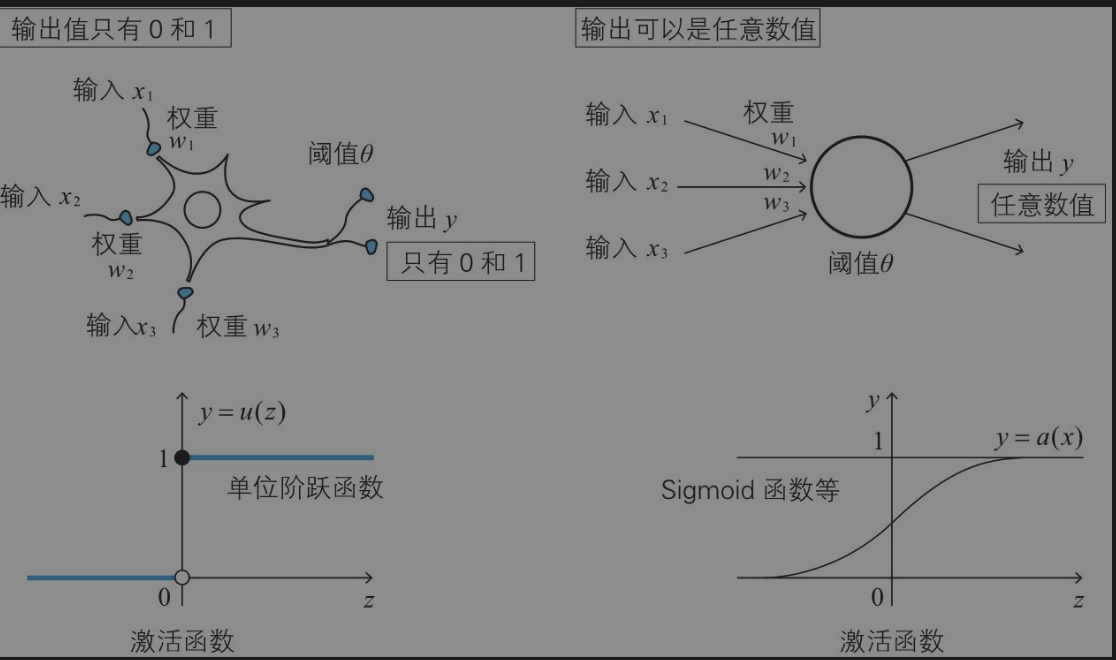
激活函数中的偏置
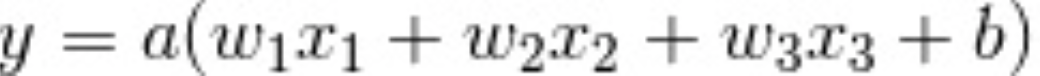
其中b做为偏置,偏置的作用调节神经单元的敏感程度,如果偏置b值较小,则神经元不容易兴奋(感觉迟钝),而如果值较大,则神经元容易兴奋(敏感)。
神经网络各层的职责
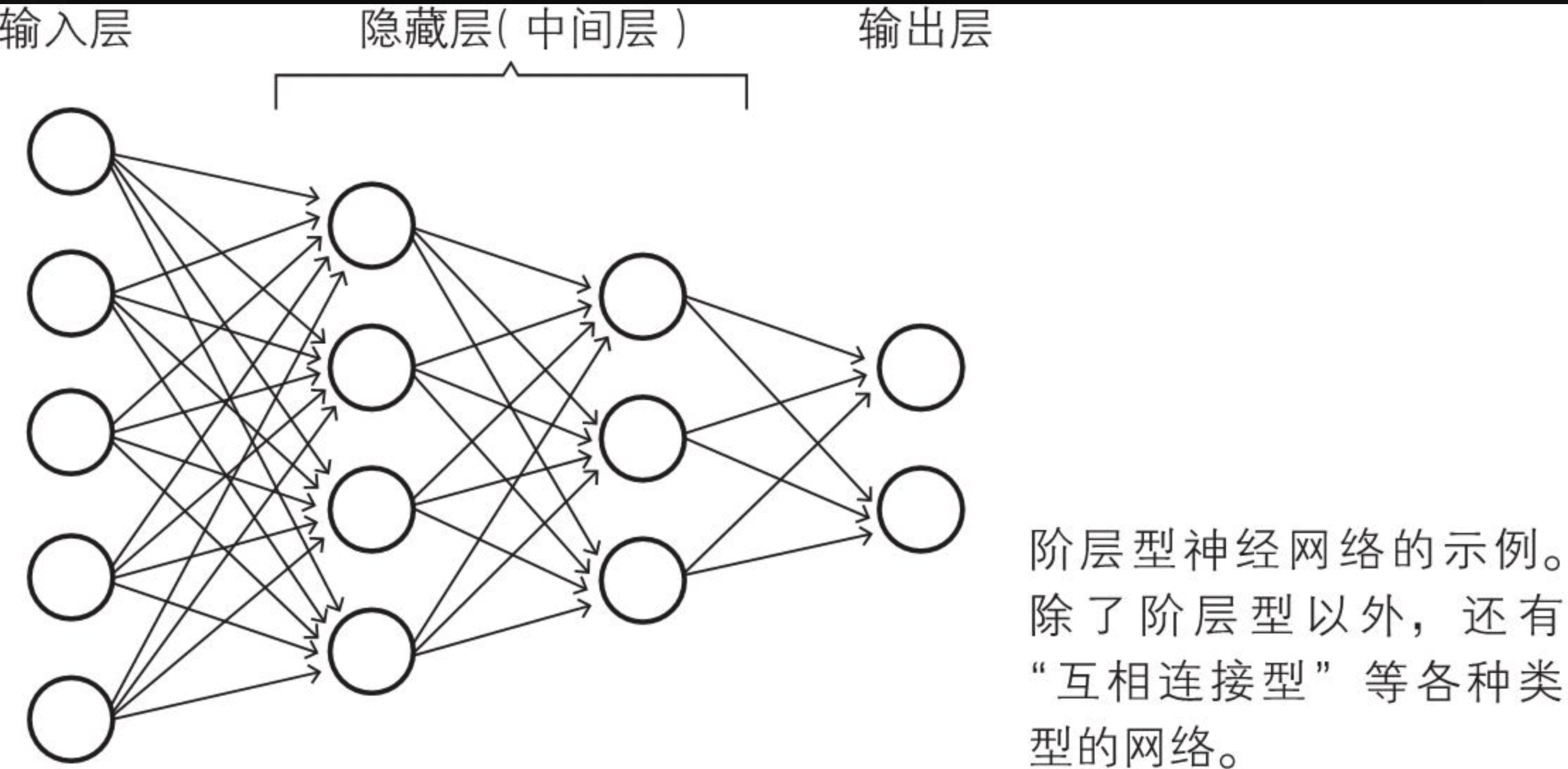
构成这个网络的各层称为输入层、隐藏层、输出层,其中隐藏层也被称为中间层。
输入层负责读取给予神经网络的信息。属于这个层的神经单元没有输入箭头,它们是简单的神经单元,只是将从数据得到的值原样输出。
隐藏层的神经单元执行前面所复习过的处理操作。在神经网络中,这是实际处理信息的部分。
输出层与隐藏层一样执行信息处理操作,并显示神经网络计算出的结果,也就是整个神经网络的输出。
前一层的神经单元与下一层的所有神经单元都有箭头连接,这样的层构造称为全连接层(fully connected layer)。
网络自学习的神经网络
有监督学习是指,为了确定神经网络的权重和偏置,事先给予数据,这些数据称为学习数据。根据给定的学习数据确定权重和偏置,称为学习。
第二章 神经网络的数学基础
原书里列出了:一次函数、二次函数、sigmod函数、正太分布的函数、连立递推式。因为这些比较简单这里不在赘述。
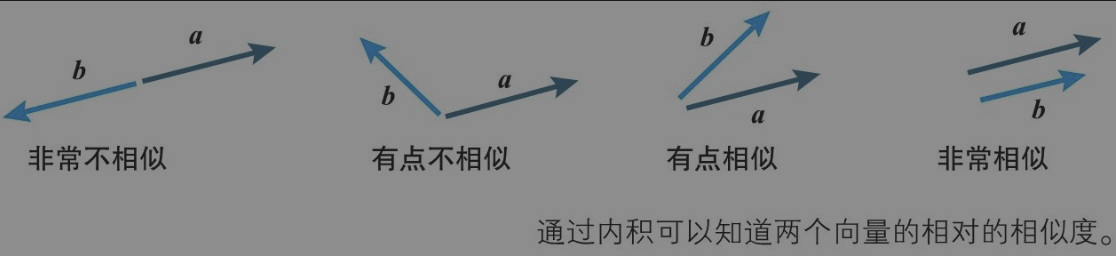
向量的内积

① 当两个向量方向相反时,内积取得最小值。
② 当两个向量不平行时,内积取平行时的中间值。
③ 当两个向量方向相同时,内积取得最大值。
内积引用:
矩阵乘积

Hadamard 乘积
对于相同形状的矩阵 A、B,将相同位置的元素相乘,由此产生的矩阵称为矩阵 A、B 的Hadamard 乘积。

矩阵的转置
矩阵的转置是一种基本的线性代数操作,它将矩阵的行变为列,列变为行。具体来说,如果你有一个m行n列的矩阵A
A = [1 2 3
4 5 6]
A^T = [1 4
2 5
3 6]
导数基础
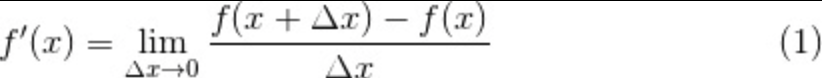
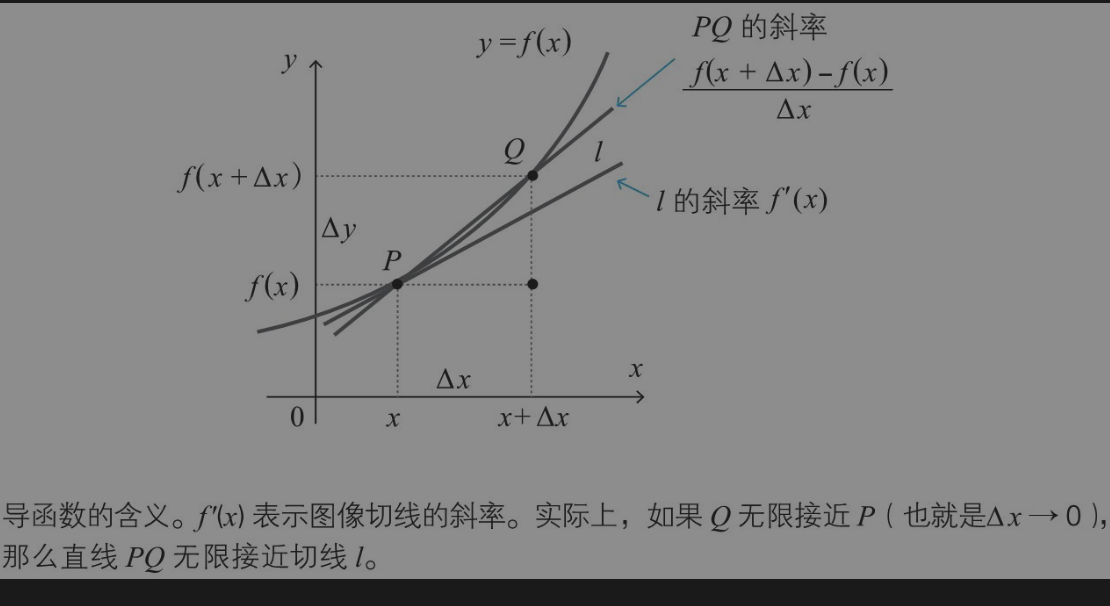
偏导数
解决多变量函数求导问题
求导的方法也同样适用于多变量函数的情况。但是,由于有多个变量,所以必须指明对哪一个变量进行求导。在这个意义上,关于某个特定变量的导数就称为偏导数。
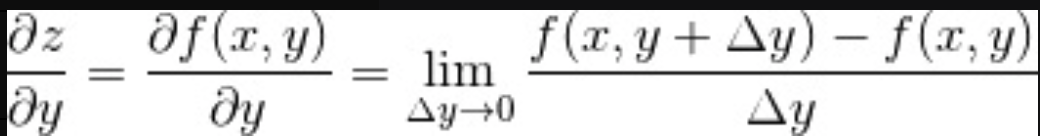
多变量函数最小值条件
光滑的单变量函数 y=f(x) 在点 x 处取得最小值的必要条件是导函数在该点取值 0。
误差反向传播法必需的链式法则
单变量函数的链式法则
已知单变量函数 y=f(u),当 u 表示为单变量函数 f=g(x)时,复合函数f(g(x)) 的导函数可以如下简单地求出来。
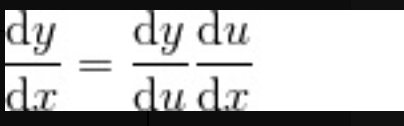
这个公式称为单变量函数的复合函数求导公式,也称为链式法则
多变量函数的链式法则
变量 z为 u、v 的函数,如果 u、v 分别为 x、y 的函数,则 z 为 x、y 的函数,此时下式(多变量函数的链式法则)成立。
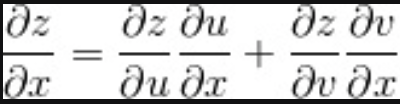
示例:
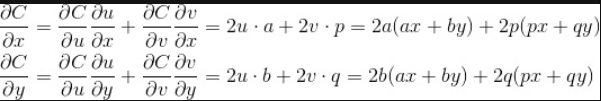
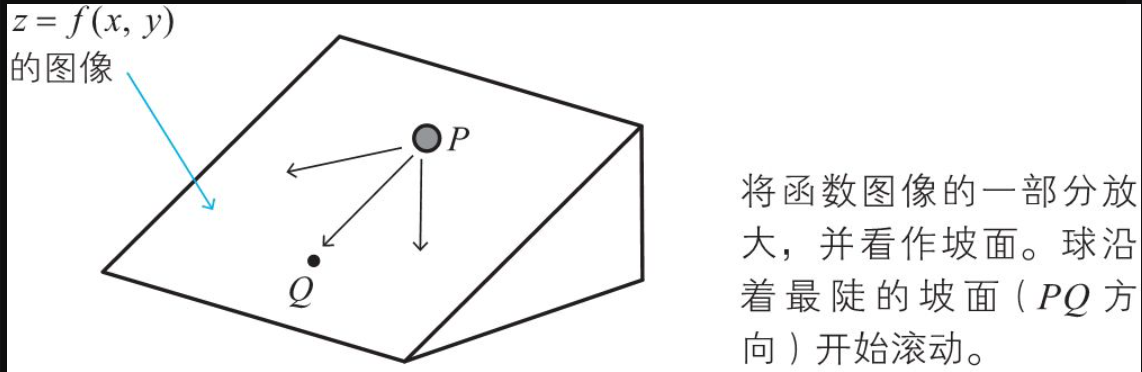
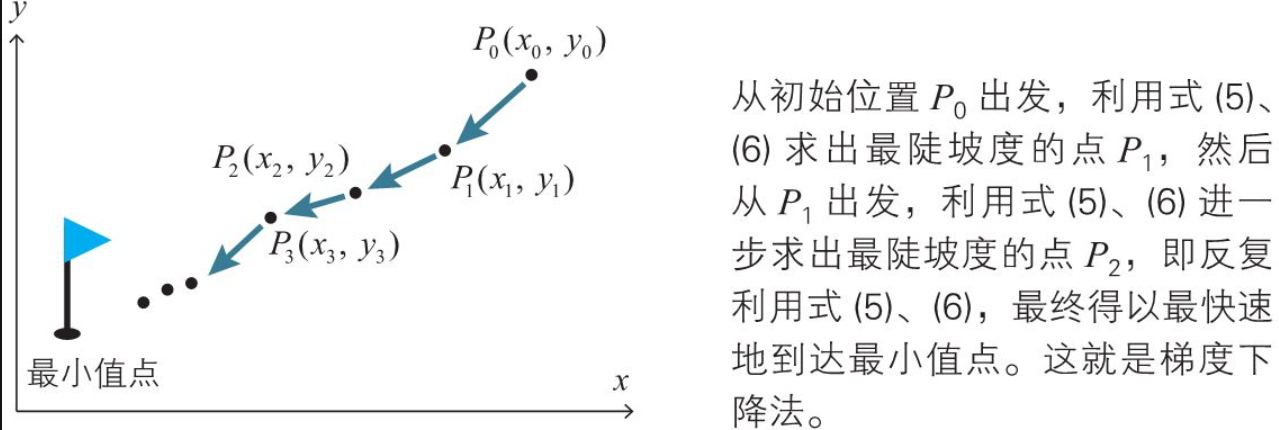
梯度下降法的思路
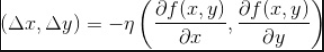
利用上述的关系式 ,如果从点 x,y 向点 x+△x, y+△移动.
ita就是我们常说的学习速率.
在函数的情况下也完全一样。要寻找函数的最小值,可以利用上述公式 找出减小得最快的方向,沿着这个方向依照上述移动公式稍微移动。在移动后到达的点处,再次利用公式算出方向,再依照上述 稍微移动。通过反复进行这样的计算,就可以找到最小值点。这种寻找函数的最小值点的方法称为二变量函数的梯度下降法。
代价函数
代价函数就是我们要求解的方程,借助链式法则来求解.在神经网络当中的代价函数就是目标函数,需要他的解趋近于0.下一章会重点做介绍
第三章 神经网络的最优化
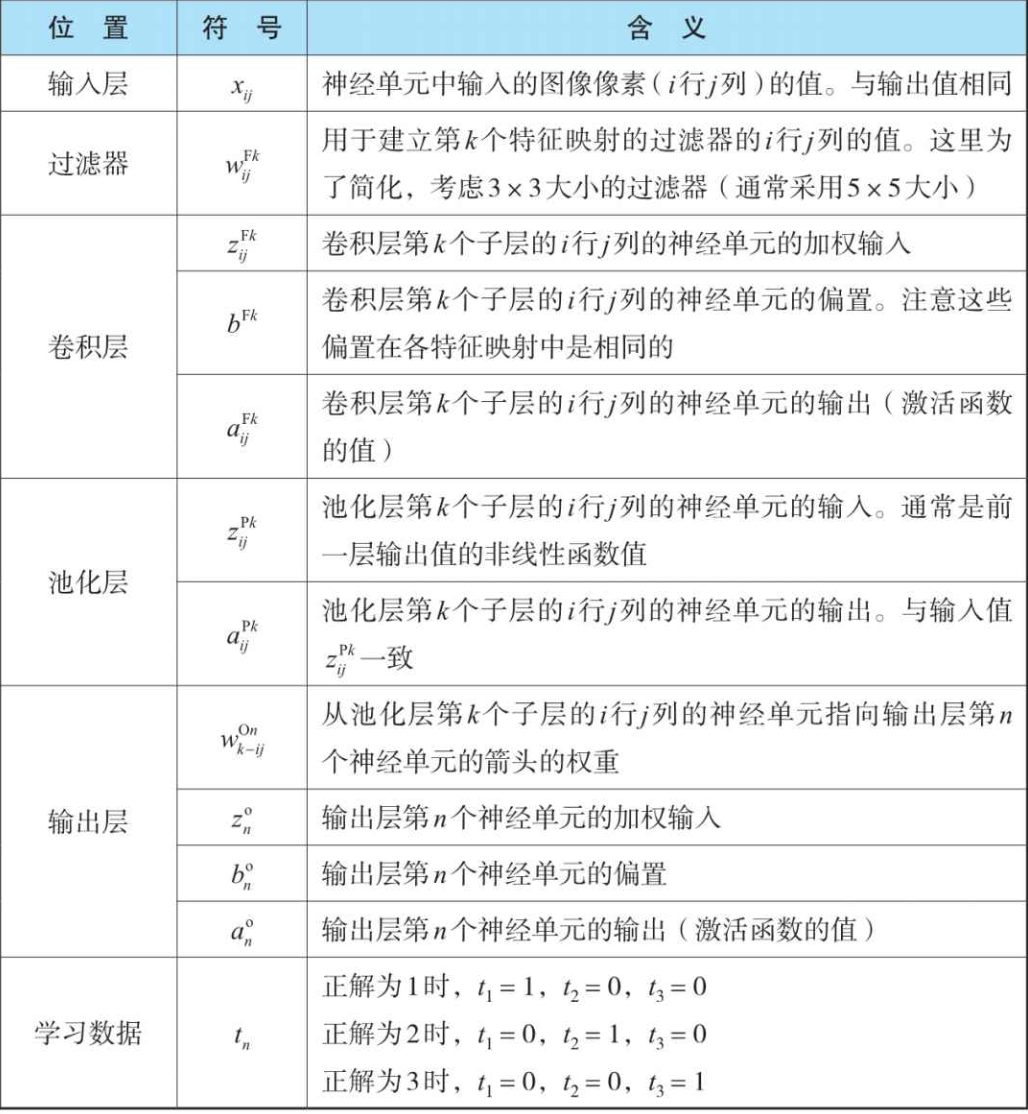
神经网络相关符号:

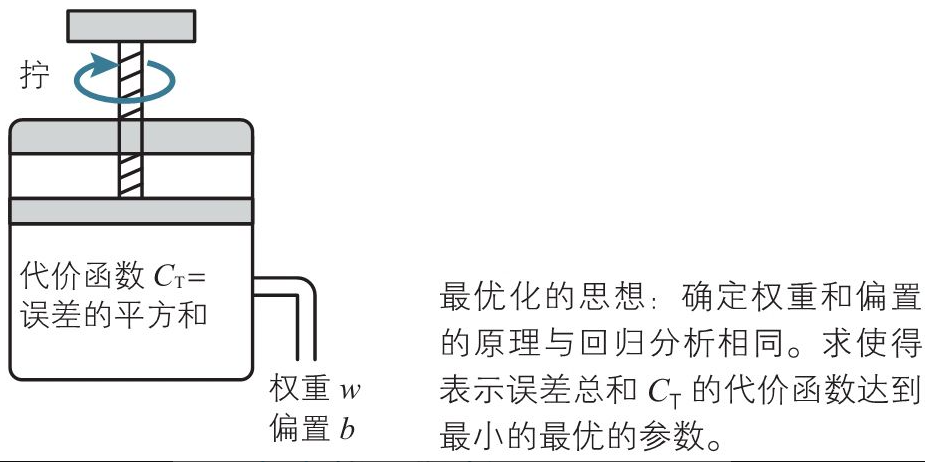
用于数据分析的数学模型是由参数确定的。在神经网络中,权重和偏置就是这样的参数。通过调整这些参数,使模型的输出符合实际的数据(在神经网络中就是学习数据),从而确定数学模型,这个过程在数学上称为最优化,在神经网络的世界中则称为学习.
输入层关系式
神经网络输入一般比较简单
隐藏层关系式
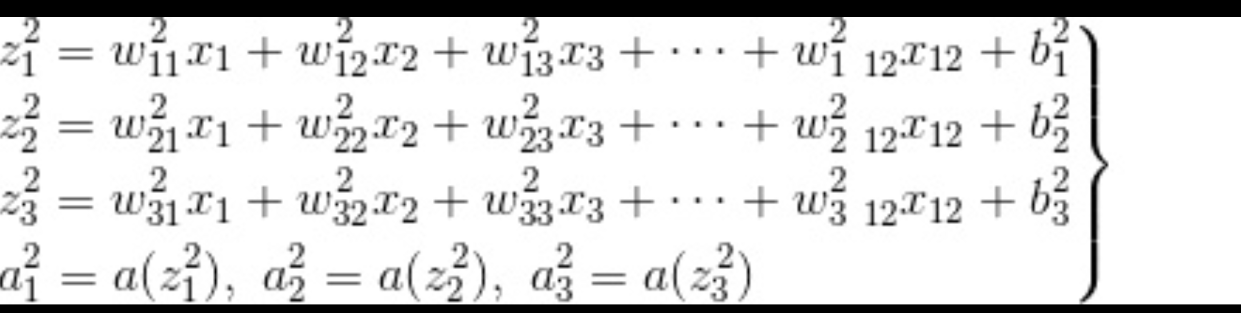
输出层关系式
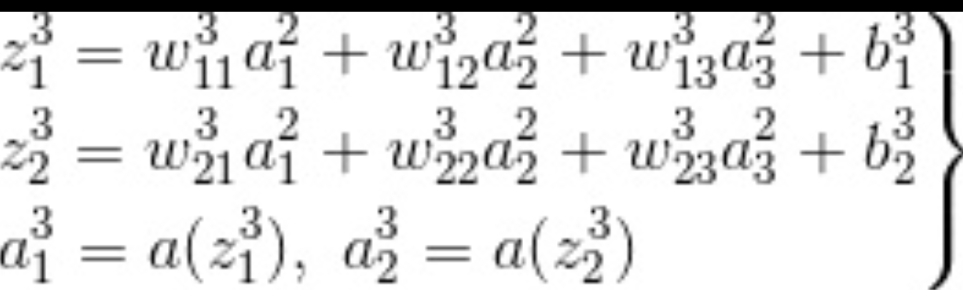
神经网络代价函数
用于数据分析的数学模型是由参数确定的。在神经网络中,权重和偏置就是这样的参数。通过调整这些参数,使模型的输出符合实际的数据(在神经网络中就是学习数据),从而确定数学模型,这个过程在数学上称为最优化(2-12 节),在神经网络的世界中则称为学习(1-7 节).
最优化的基础:代价函数的最小化
代价函数
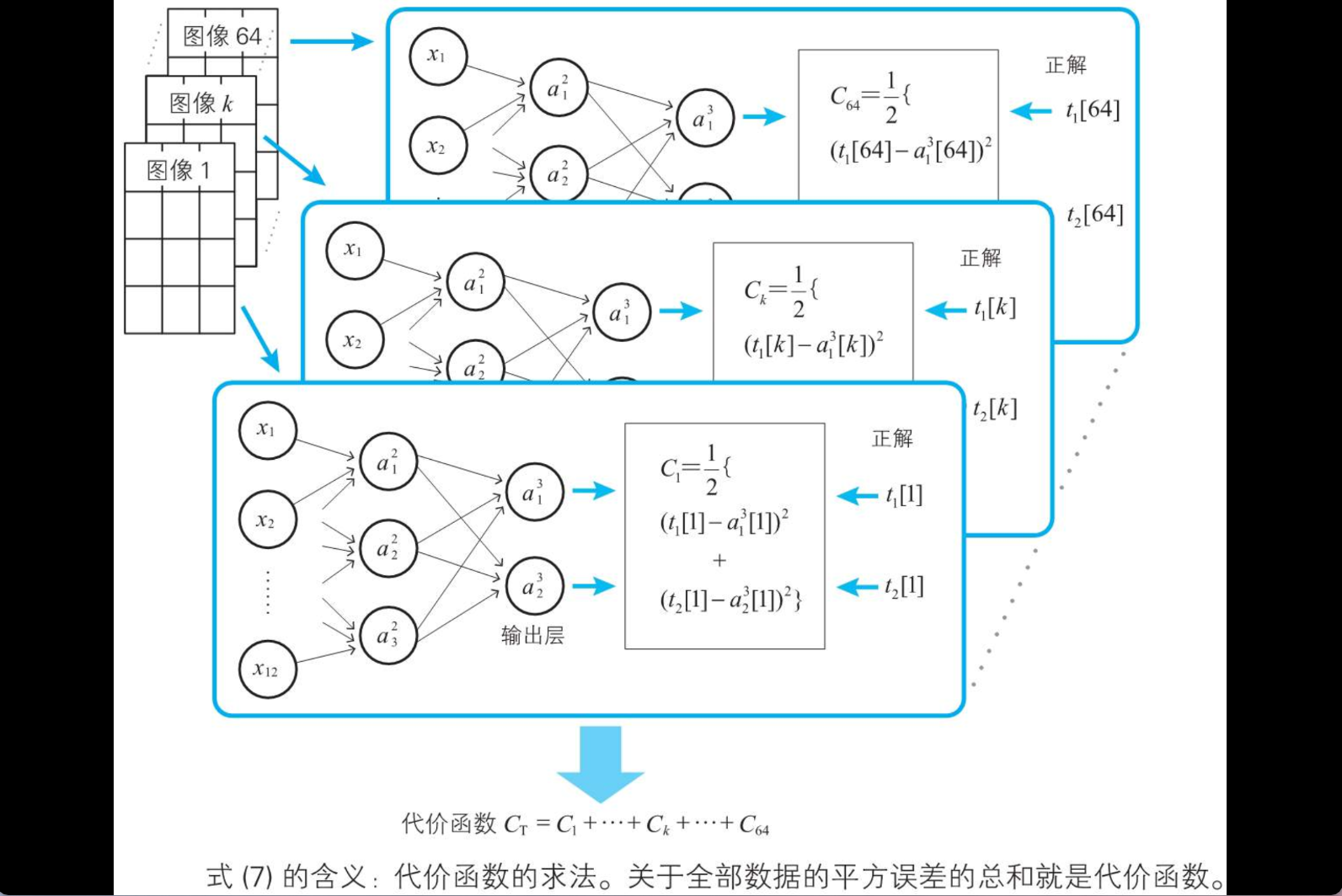
第四章 神经网络和误差反向传播法
神经网络传播
根据梯度下降法的规则,计算成本是特别高的,导致我们计算目标函数和要计算的变量的梯度成本特别高昂.
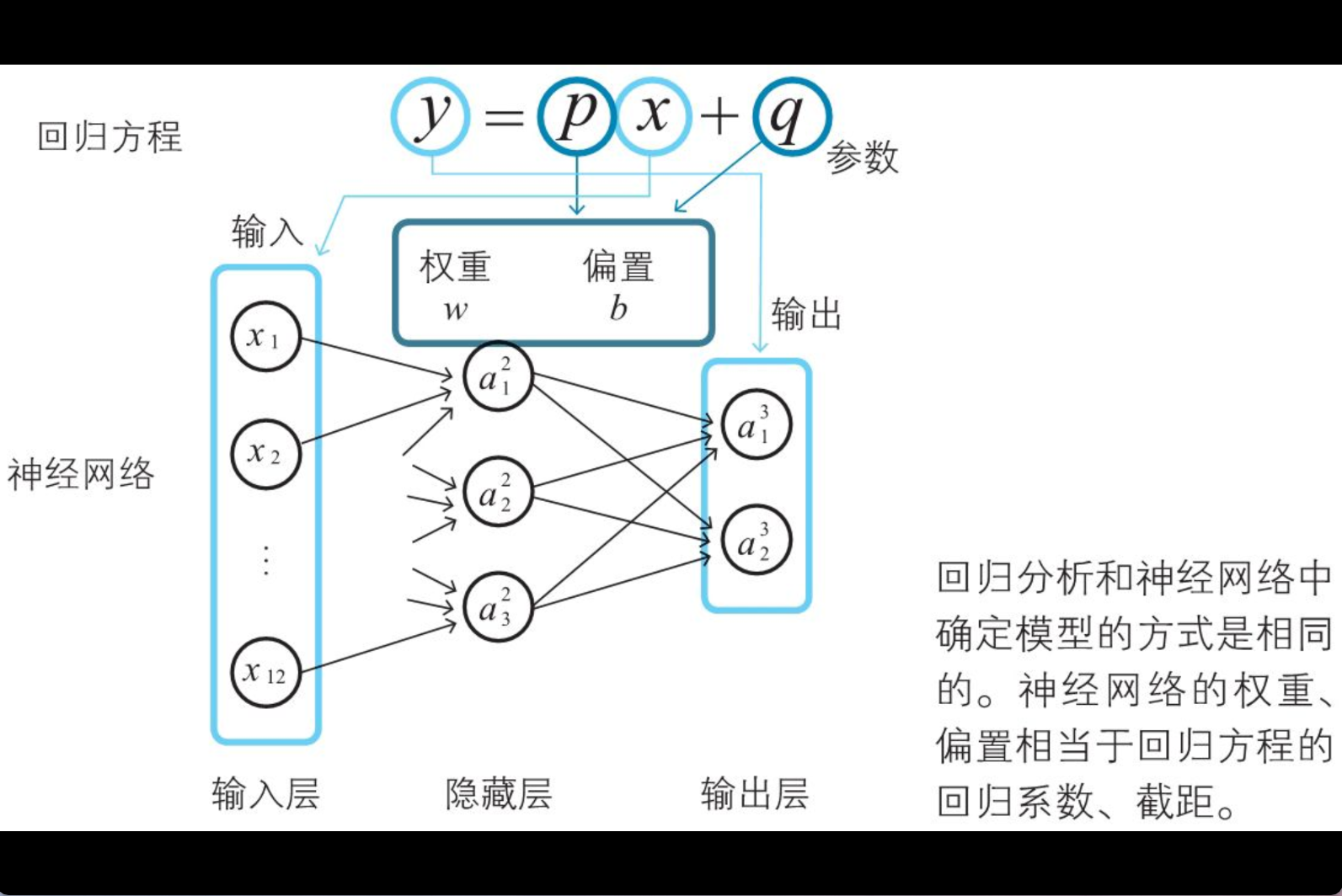
神经网络和回归分析的差异
(i) 相比回归分析中使用的模型的参数,神经网络中使用的参数的数目十分巨大。(ii) 线性回归分析中使用的函数为一次式,而神经网络中使用的函数(激活函数)不是一次式。因此,在神经网络的情况下,代价函数变得很复杂。
反向传播法解决的实际问题
在神经网络中,我们需要计算损失函数关于网络参数的梯度,这个梯度告诉我们应该如何调整参数以减小损失。但是,直接计算这个梯度在计算上是非常昂贵的,特别是对于深度神经网络.
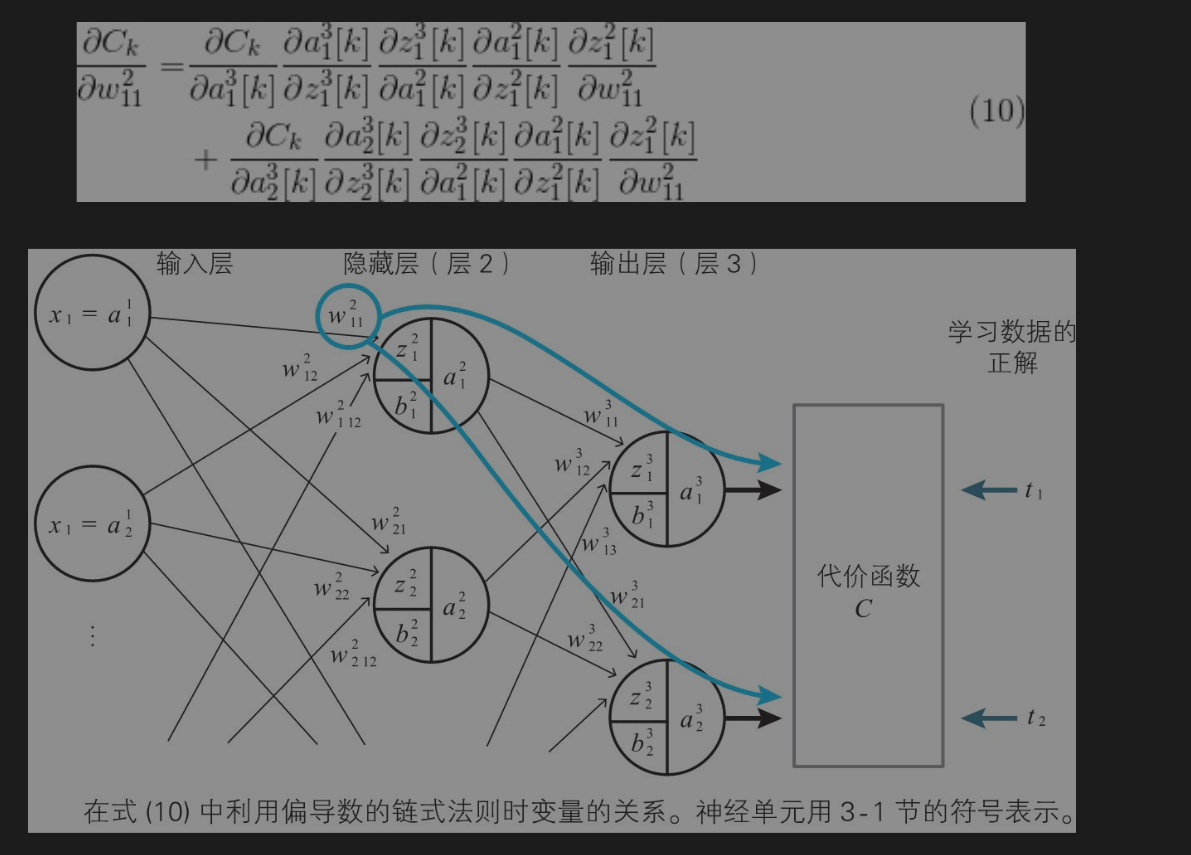
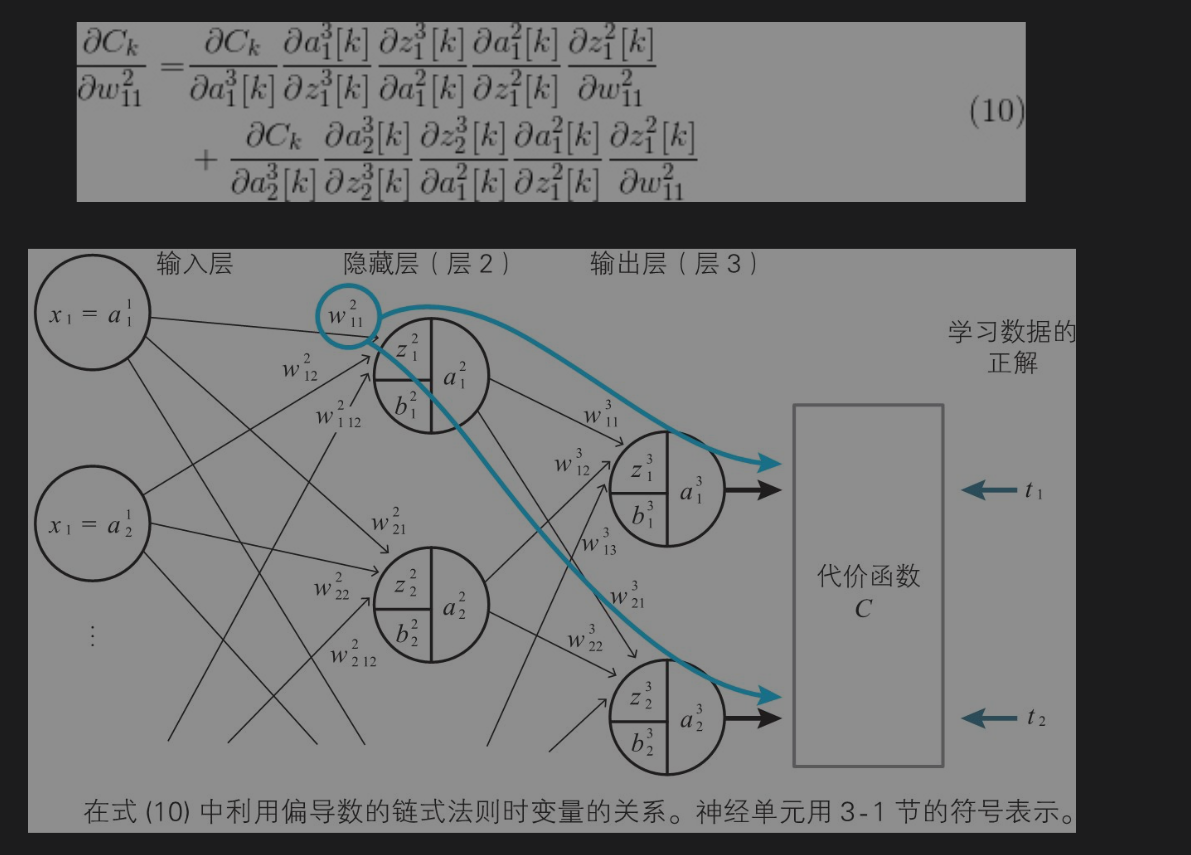
神经单元误差

称为神经单元误差的含义。从这个定义表示神经单元的加权输入给平方误差带成的变化率。称为神经单元误差的含义。从这个定义表示神经单元的加权输入给平方误差带成的变化率。
引入的神经单元误差的递推关系式,通过这些递推关系式来回避复杂的导数计算。
得到神经单元误差后,通过这样的公式得到各个参数的梯度,得到个参数的梯度后就可以结合学习率更新对应的权重,偏置值.
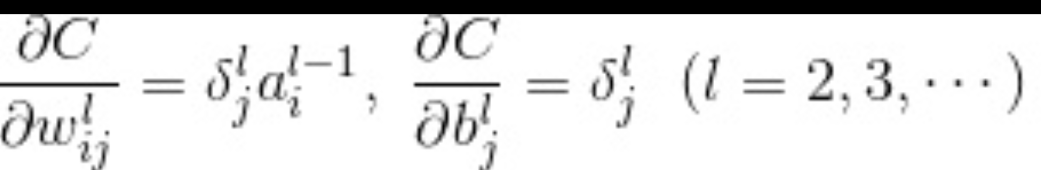
各层神经误差的计算
输出层
a 为激活函数,c为目标函数
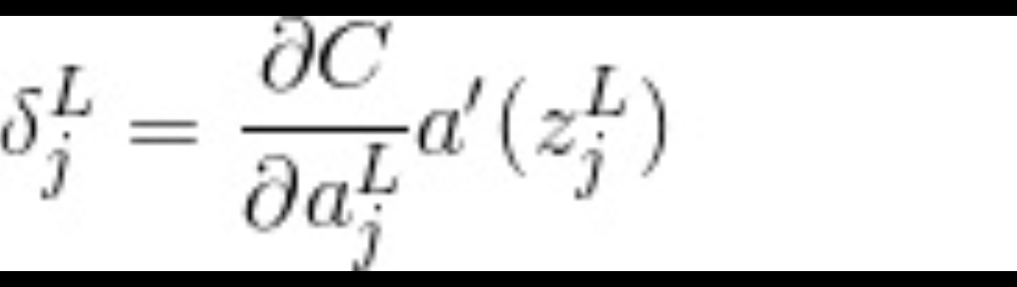
中间层不求导可得到值
中间层递推方式
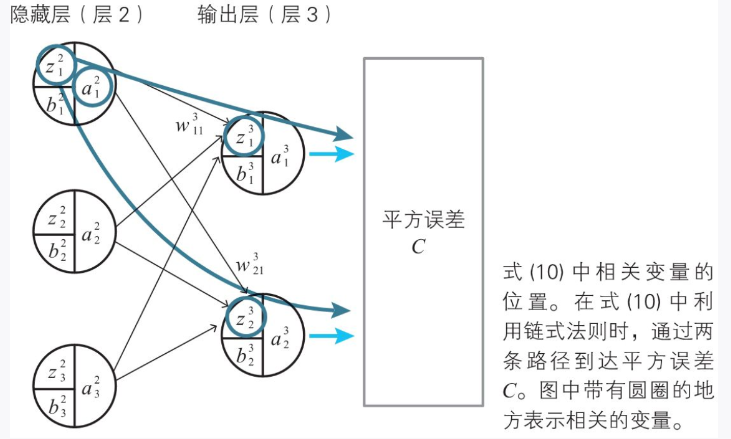
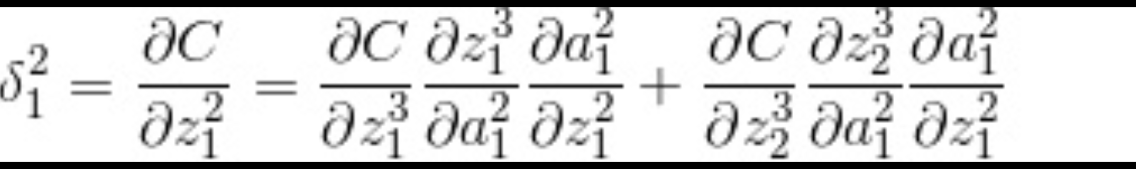
可带入得出:
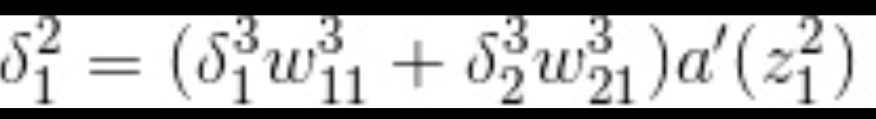
最终的递推关系式:
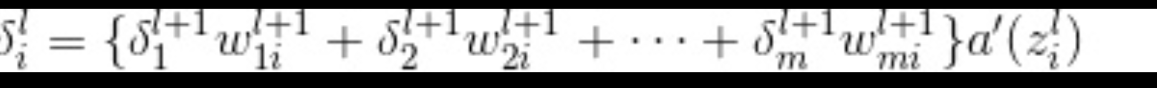
l为2以上的整数.
第五章 深度学习和卷积网络
卷积网络的结构
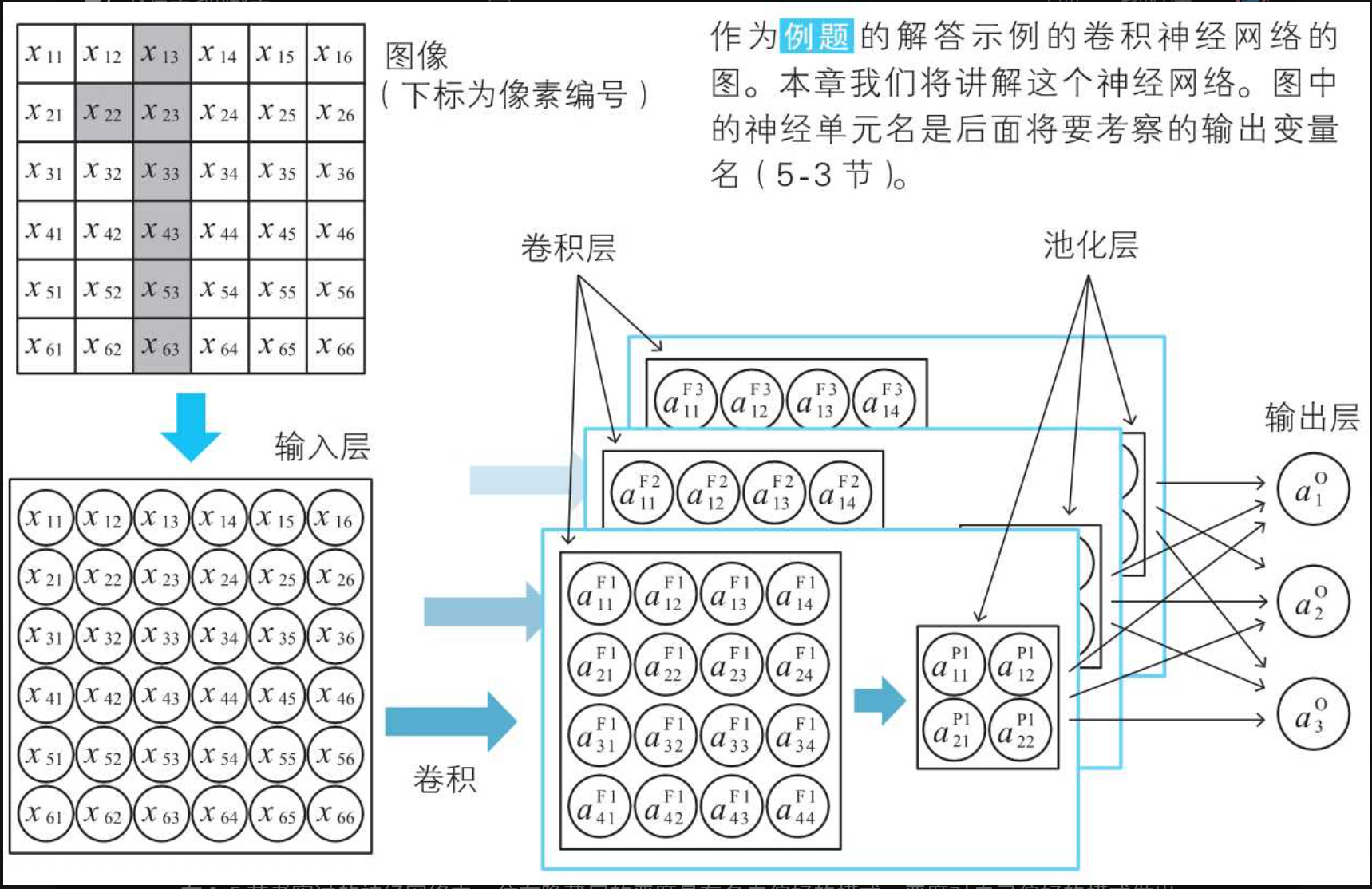
池化层的神经单元中浓缩了作为考察对象的图像中包含了多少激活函数的模式这一信息
通过池化进行信息压缩
使用过滤器过滤图像。
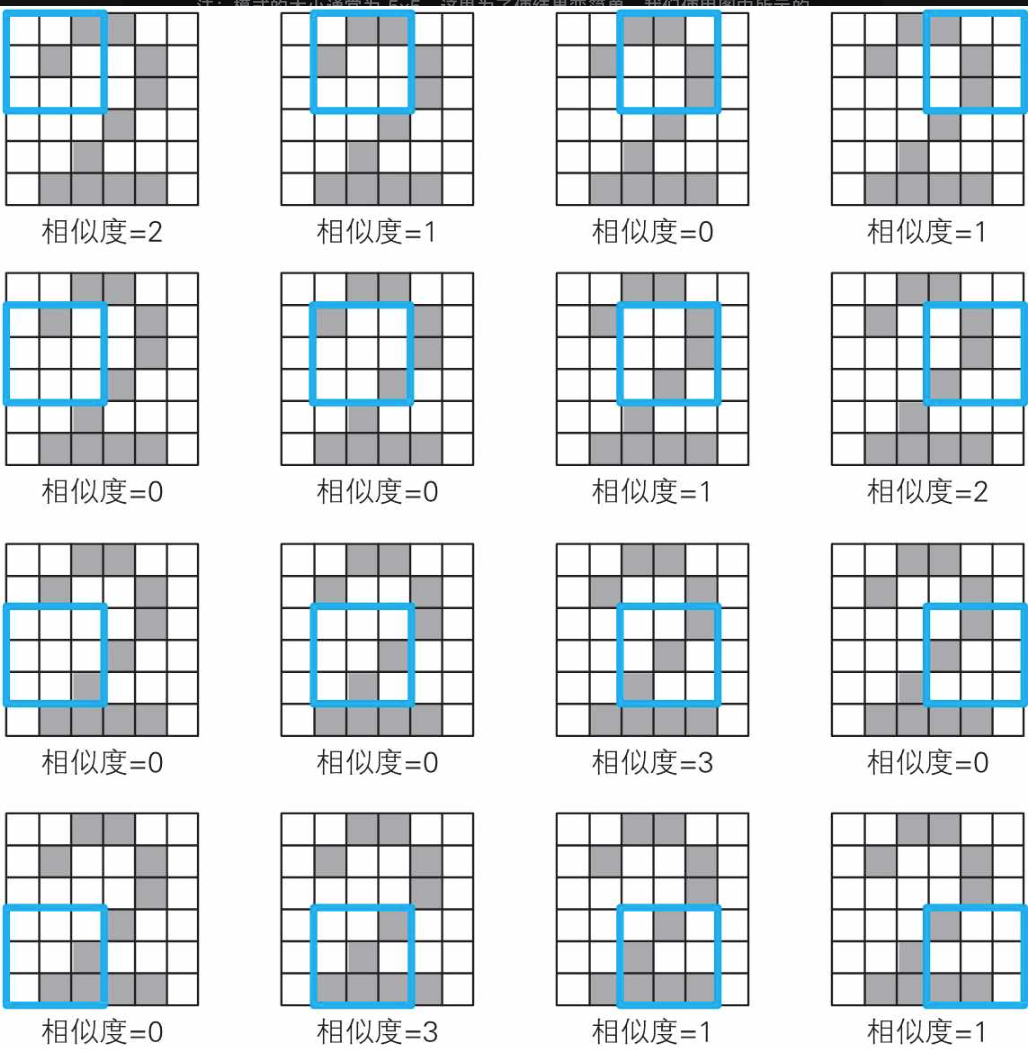
我们将这个相似度汇总一下,如下表所示。这就是根据过滤器 S 得到的卷积(convolution)的结果,称为特征映射(feature map)。
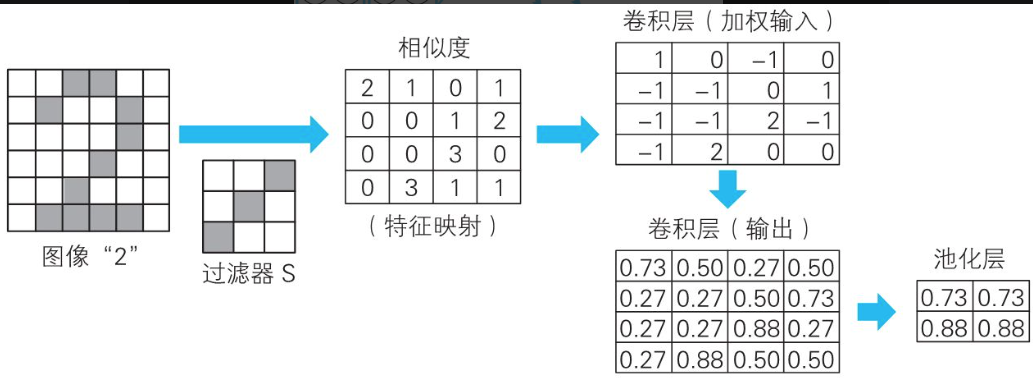
书中我们使用最有名的信息压缩方法最大池化(max pooling),具体来说就是将划分好的各区域的最大值提取出来。
神经网络的变量关系式
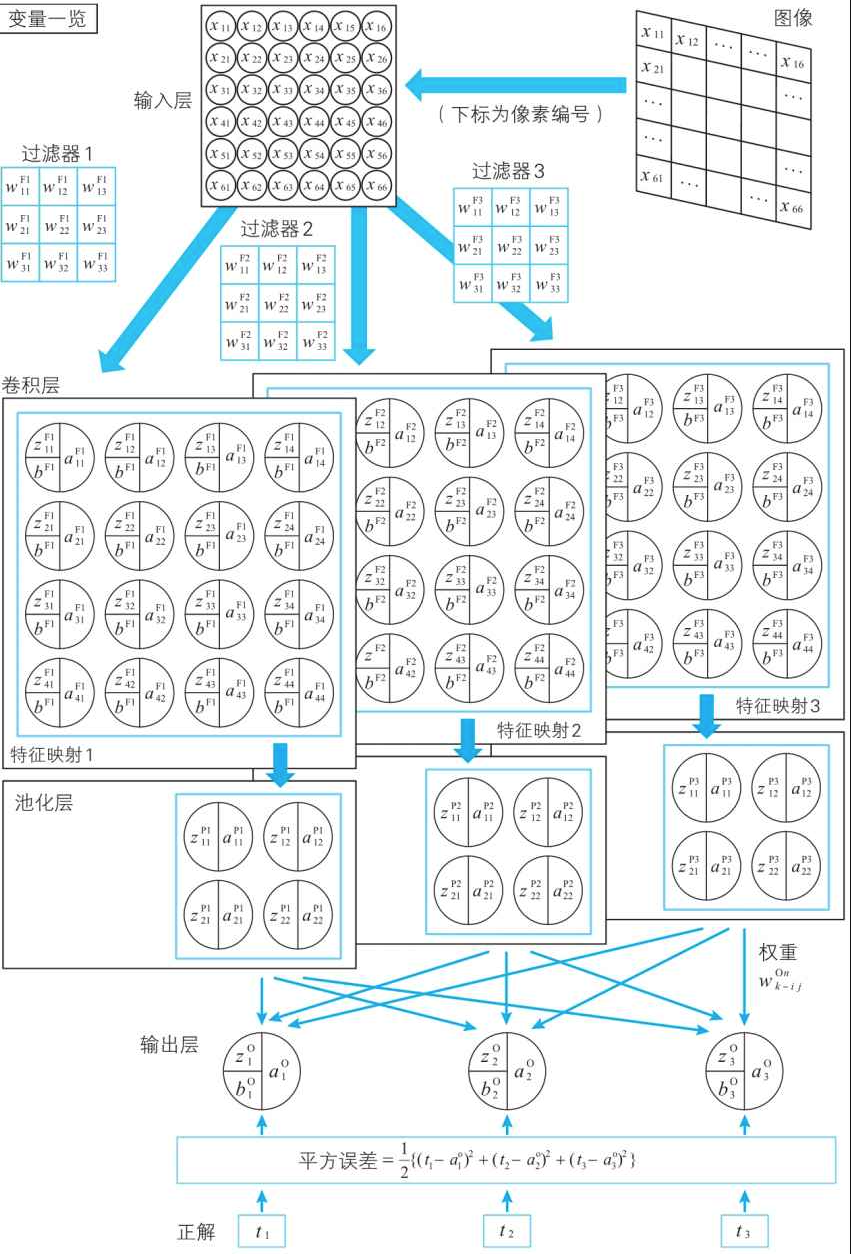
卷积层内部每个本质还是神经单元,这张图很好了说明卷积内部和神经网络之间的关系。
过滤器和卷积层
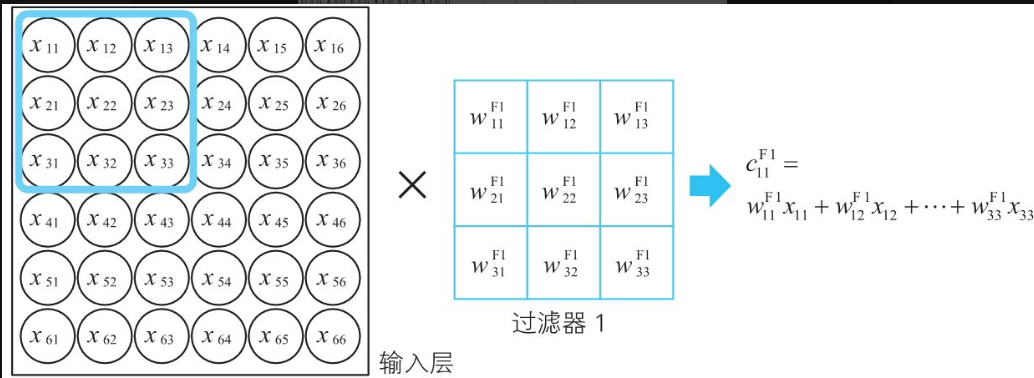
过滤器输出和卷成的输入的关系式子:
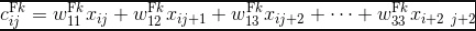
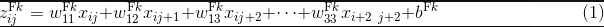
池化层
最大池化层

从神经网络的观点来看,池化层也是神经单元的集合。不过,从计算方法可知,这些神经单元在数学上是非常简单的。通常的神经单元是从前一层的神经单元接收加权输入,而池化层的神经单元不存在权重和偏置的概念,也就是不具有模型参数。
卷积的反向误差方式
重点讲一下和第四章一般的反向误差的区别:
各个层的公式:
卷积层:
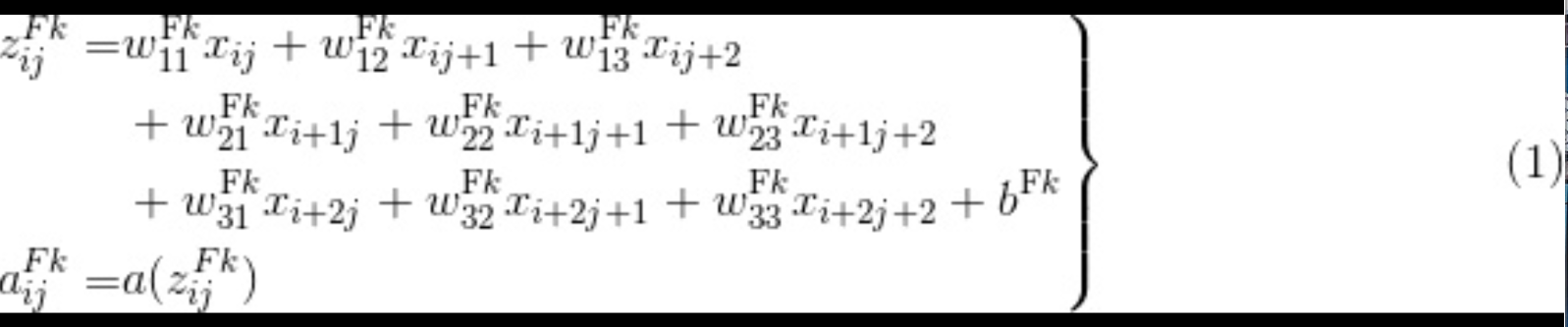
池化层:

输出层: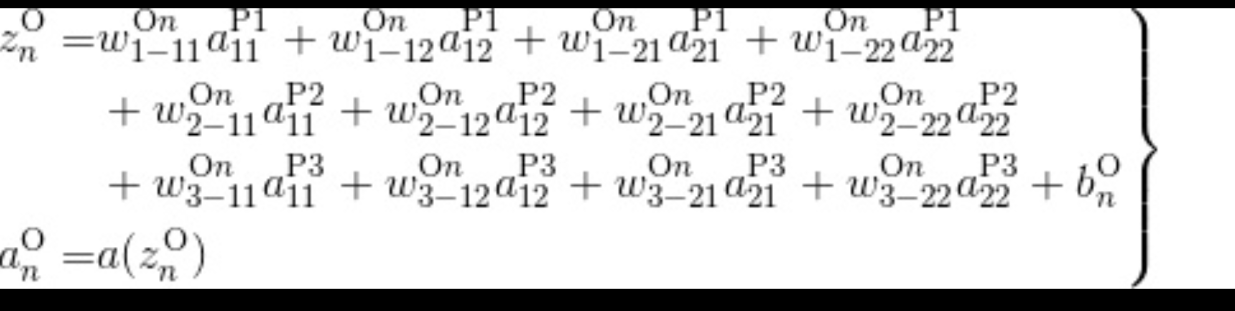
- 最大池化的偏导,卷积层输出是最大值那么值为1否则就是0


- 输出层和第四章基本一致
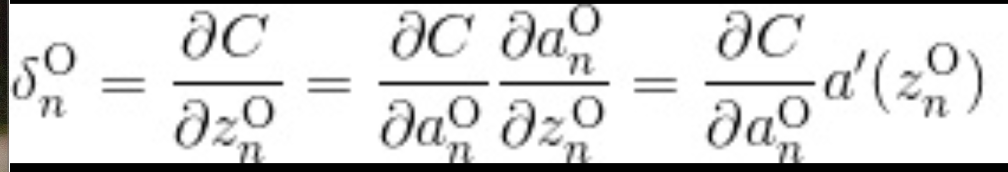
总结
整本书对深度学习的基本概念做了详细的介绍,对所用到数学信息做了深入的介绍,尤其是对误差反向传播法的概念做了深入的讲解.正本书对我们理解深度学习中的概念有着重要的意义,建议详细做阅读.是一本非常不错的书籍.